Deep Convolutional Neural Networks: DenseNet

Problem with traditional Convolutional Neural Networks

Convolutional Neural Networks are the popular choice of neural networks for different Computer Vision tasks such as image recognition. The problems arise with CNNs when they go deeper. This is because the path for information from the input layer until the output layer (and for the gradient in the opposite direction) becomes so big, that they can get vanished before reaching the other side.

How ResNet works?

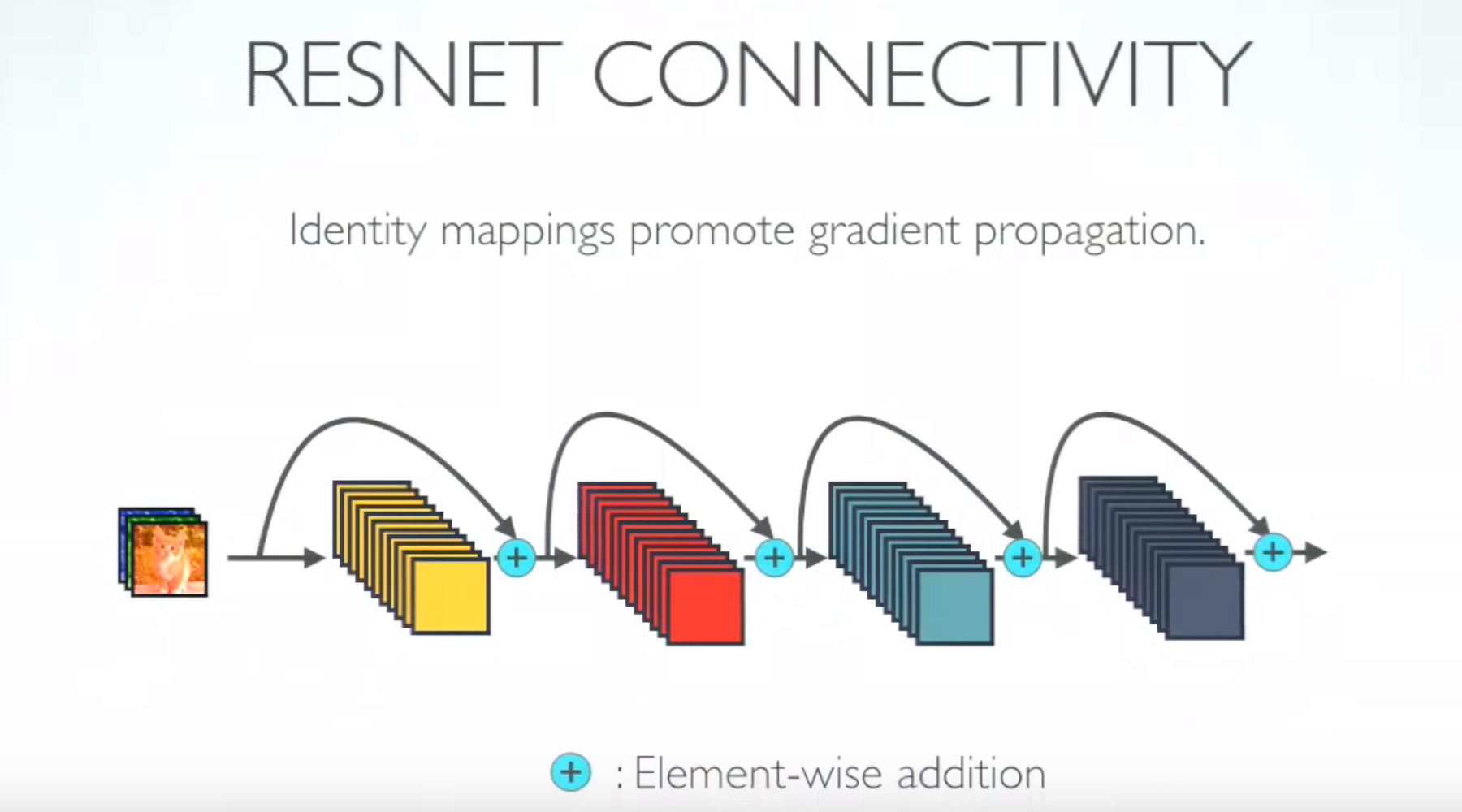
ResNet was introduced few years ago to solve this problem. The core idea behind the ResNet is “identity shortcut connection” that skips one or more layers, as shown in the following figure.

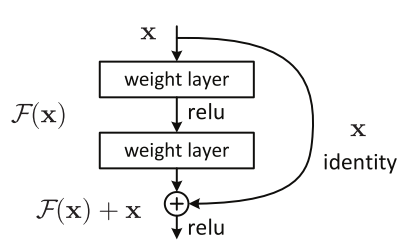
Neural networks are universal function approximators and that the accuracy increases with increasing number of layers. But there is a limit to the number of layers added that result in accuracy improvement. So, if neural networks were universal function approximators then it should have been able to learn any simplex or complex function. But it turns out to problems such as vanishing gradients and curse of dimensionality.

At this point a shallow network are learns better than their deeper counterparts. So, if can skip few layers intelligently using skip connections or residual connections our problem is solved.

DenseNet

Gao Huang et al. introduced Dense Convolutional networks. DenseNets have several compelling Advantages:

• alleviate the vanishing-gradient problem
• strengthen feature propagation
• encourage feature reuse, and substantially reduce the number of parameters.

ResNet vs DenseNet

DenseNet is also a variation of ResNet. A layer in dense receives all the outs of previous layers and concatenate them in the depth dimension. In ResNet, a layer only receives outputs from the previous second or third layer, and the outputs are added together on the same depth, therefore it won’t change the depth by adding shortcuts. In ResNet the output of layer of k is

ResNet: x[k] = f(w * x[k-1] + x[k-2])

DenseNet: x[k] = f(w * H(x[k-1], x[k-2], … x[1]))

where H means stacking over the depth dimension. 

Resources & Acknowledgements

https://theailearner.com/2018/12/09/densely-connected-convolutional-networks-densenet/

https://towardsdatascience.com/residual-blocks-building-blocks-of-resnet-fd90ca15d6ec/

[https://medium.com/@smallfishbigsea/densenet-2b0889854a92/] (https://medium.com/@smallfishbigsea/densenet-2b0889854a92/)